 |
| BILANGAN BULAT |
• Bulat positif (1, 2, 3, 4, 5, …)• Nol : 0
• Bulat Negatif ( …,-5,-4,-3,-2,-1)
Himpunan Bilangan bulat
A = { …, -4, -3, -2, -1, 0, 1, 2, 3, 4, … }
Di dalam bilangan
bulat terdapat bilangan genap dan
ganjil :
Bilangan yang habis dibagi dengan 2
• Bilangan bulat genap { …, -6, -4, -2, 0, 2, 4, 6, … }
Bilangan yang habis dibagi dengan 2
• Bilangan bulat ganjil { …, -5, -3, -1, 1, 3, 5, … }
Bilangan yang apabila dibagi 2 tersisa -1 atau 1
B. Operasi Hitung Pada Bilangan Bulat :
• Penjumlahan dan Sifat-sifatnya
1. Sifat Asosiatif
( a + b ) + c = a + ( b + c )
Contoh :
(5 + 3 ) + 4 = 5 + ( 3 + 4 ) = 12
2. Sifat Komutatif a + b = b + a
Contoh :
7 + 2 = 2 + 7 = 9
3. Unsur Identitas terhadap penjumlahan
Bilangan Nol (0) disebut unsur identitas atau netral terhadap penjumlahan
a + 0 = 0 + a
Contoh :
6 + 0 = 0 + 6
4. Unsur invers terhadap penjumlahan
Invers jumlah (lawan) dari a adalah
-a
Invers jumlah (lawan) dari – a adalah a
a + (-a) = (-a) + a
a + (-a) = (-a) + a
contoh
:
5. Bersifat tertutup
Apabila dua buah bilangan bulat ditambahkan maka hasilnya adalah
5 + (-5) = (-5) + 5 =
5. Bersifat tertutup
Apabila dua buah bilangan bulat ditambahkan maka hasilnya adalah
bilangan bulat juga.
a dan b ∈ bilangan bulat maka a + b = c ; c ∈ bilangan bulat
contoh :
4 + 5 = 9 ; 4,5,9 ∈ bilangan bulat
• Pengurangan dan Sifat-sifatnya
1. Untuk sembarang bilangan bulat berlaku :
a – (-b) = a + b
contoh:
8 – 5 = 8 + (-5) = 3
7 – (-4) = 7 + 4 = 11
2. Sifat Komutatif dan asosiatif tidak berlaku
a – b ≠ b - a
4 + 5 = 9 ; 4,5,9 ∈ bilangan bulat
• Pengurangan dan Sifat-sifatnya
1. Untuk sembarang bilangan bulat berlaku :
a – b = a + (-b)
a – (-b) = a + b
contoh:
8 – 5 = 8 + (-5) = 3
7 – (-4) = 7 + 4 = 11
2. Sifat Komutatif dan asosiatif tidak berlaku
a – b ≠ b - a
(a – b ) – c ≠ a – ( b – c )
Contoh :
7 – 3 ≠ 3 -7 Æ 4 ≠ - 4
(9 – 4) – 3 ≠ 9 – (4-3) → 2 ≠ 8
3. Pengurangan bilangan nol mempunyai sifat :
a – 0 = a dan 0 – a = -a
4. Bersifat tertutup, yaitu bila dua buah bilangan bulat dikurangkan
hasilnya adalah bilangan bulat juga : a dan b ∈ bilangan bulat
maka a - b =
c ;
c ∈ bilangan bulat
contoh :
7 - 8 = -1 ; 7,8,-1 ∈ bilangan bulat
• Perkalian dan Sifat-sifatnya
1. a x b = ab → hasil perkalian dua bilangan bulat positif adalah bilangan bulat positif
Contoh: 7 x 6 = 6 x 7 = 42
a x –b = -ab → hasil pekalian bilangan bulat positif dan negatif hasilnya adalah bilangan bulat negatif
Contoh : 3 x -4 = -12
-a x -b = ab → hasil perkalian dua bilangan negatif adalah bilangan bulat positif
Contoh : -4 x -5 = 20
2. Sifat Asosiatif
(a x b) x c = a x (b x c)
Contoh: (2 x 3) x 4 = 2 x (3x4) = 24
3. Sifat komutatif
a x b = b x a
Contoh : 5 x 4 = 4 x 5 = 20
4. Sifat distributif
a x (b+c) = (a x b ) + (a x c)
Contoh : 3 x ( 2 +6) = (3 x 2) + (3 x 6) = 24
5 Unsur identitas untuk perkalian
4. Sifat distributif
a x (b+c) = (a x b ) + (a x c)
Contoh : 3 x ( 2 +6) = (3 x 2) + (3 x 6) = 24
5 Unsur identitas untuk perkalian
- hasil perkalian bilangan bulat dengan nol hasilnya adalah bilangan nol
a x 0 = 0
- hasil perkalian bilangan bulat dengan 1 hasilnya adalah bilangan bulat itu juga
- hasil perkalian bilangan bulat dengan 1 hasilnya adalah bilangan bulat itu juga
a x 1 = 1 x a = a
6. Bersifat tertutup
Jika dua bilangan bulat dikalikan maka hasilnya adalah bilangan bulat juga
6. Bersifat tertutup
Jika dua bilangan bulat dikalikan maka hasilnya adalah bilangan bulat juga
a x b = c ; a, b, c ∈ bilangan bulat
• Pembagian dan Sifat-sifatnya
1. Hasil bagi dua bilangan bulat positif adalah bilangan positif
(+) : (+) = (+)
• Pembagian dan Sifat-sifatnya
1. Hasil bagi dua bilangan bulat positif adalah bilangan positif
(+) : (+) = (+)
Contoh : 8 : 2 = 4
2. Hasil bagi dua bilangan bulat negatif adalah bilangan positif
2. Hasil bagi dua bilangan bulat negatif adalah bilangan positif
(-) : (-) = (+)
Contoh : -10 : -5 = 2
3. Hasil bagi
dua bilangan bulat yang berbeda
adalah bilangan negatif
(+) : (-) = (-) (-) : (+) = (-)
(+) : (-) = (-) (-) : (+) = (-)
Contoh : 6 : -2 = -3
4.
Hasil bagi bilangan bulat dengan 0 (nol) adalah tidak terdefinisi
-12 : 3 = -4
a : 0 → tidak terdefinisi
(~)
Contoh : = ~ (Tidak terdefinisi)
5. Tidak berlaku sifat komutatif dan asosiatif
0 : a → 0 (nol)
Contoh : = ~ (Tidak terdefinisi)
5. Tidak berlaku sifat komutatif dan asosiatif
(8 : 2) : 4 ≠ 8 : (2 : 4) ⟶ 1≠ 16
6. Bersifat tidak tertutup
Jika dua bilangan bulat dibagi hasilnya belum
tentu bilangan bulat
juga
contoh : 6 : 2 = 3 ⟶ bilangan bulat
 ⟶ bukan bilangan bulat (bilangan pecahan)
⟶ bukan bilangan bulat (bilangan pecahan)
contoh : 6 : 2 = 3 ⟶ bilangan bulat
• Pemangkatan bilangan bulat
Contoh :
43 = 4 x 4 x 4 = 64
35 = 3 x 3 x 3 x 3 x 3 = 243
• Akar pangkat dua dan akar pangkat tiga bilangan bulat
1. Akar kuadrat (akar pangkat dua)
2. Akar kubik (akar pangkat tiga)



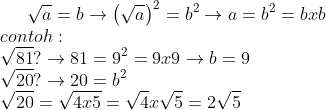




Tidak ada komentar:
Posting Komentar