Pengertian Matriks

Matriks adalah kumpulan bilangan, simbol, atau ekspresi yang disusun membentuk persegi panjang berdasarkan baris dan kolom. Notasi matriks dinyatakan dalam huruf kapital. Berikut ini contoh penulisan matriks.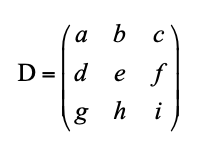

Matriks D di atas memiliki sembilan elemen, yaitu a–i.Letak elemen dinyatakan dalam fungsi x_p,qdi mana pmenunjukkan baris, sedangkan qmenunjukkan kolom, contohnya x_2,3= f; x_3,1=g; dan x_2,2= e. Baris merupakan bagian matriks yang mengarah horizontal, sedangkan kolom merupakan bagian matriks yang mengarah vertikal.

Ordo Matriks

Ordo atau ukuran matriks menunjukkan banyaknya baris dan kolom di dalam matriks. Ordo biasa dinotasikan sebagai  ∑ baris x kolom. Perhatikan contoh berikut.

Bagaimana Quipperian, sudah paham tentang ordo matriks, belum? Jika sudah, selanjutnya Quipper Blog akan membahas tentang transpose matriks.

Transpose Matriks

Transpose matriks merupakan bentuk operasi matriks di mana susunan baris diubah menjadi kolom, sedangkan bagian kolom diubah menjadi baris. Baris ke-pdiubah menjadi kolom ke-patau kolom ke-qdiubah menjadi baris ke-q. Jika matriks D di atas dijadikan transpose matriks D, notasi yang digunakan adalah D^T. Untuk lebih jelasnya, perhatikan contoh berikut.

Berdasarkan transpose matriks di atas, Quipperian bisa melihat bahwa elemen baris ke-1, yaitu 1, 2, 3, dituliskan pada kolom ke-1, elemen baris ke-2, yaitu 4, 5, 6, dituliskan pada kolom ke-2, dan begitu seterusnya. Dengan demikian, transpose matriks bisa mengubah ordo matriks jika jumlah baris dan kolomnya tidak sama.

Matriks Sama

Suatu matriks dikatakan sama jika matriks-matriks tersebut memiliki ordo yang sama dan setiap elemennya terletak pada baris dan kolom yang sama. Jika suatu matriks sama, otomatis setiap elemen yang seletak nilainya sama. Perhatikan contoh soal berikut.

Contoh Soal 1

Diketahui dua matriks sebagai berikut.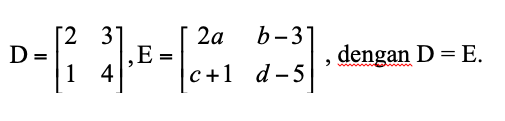

Tentukan nilai dari a, b,c, dan d!
Pembahasan:
Untuk mencari nilai a, b,c, dan d, Quipperian harus tahu bahwa matriks D = E, sehingga elemen seletak nilainya pasti sama.

Dari perhitungan di atas, diperoleh nilai a= 1, b = 6, c= 0, dan d= 9.
Jadi, nilai a, b,c, dan dberturut-turut adalah 1, 6, 0, dan 9.

Operasi Antarmatriks

Layaknya bilangan, matriks juga bisa dioperasikan seperti penjumlahan, pengurangan, perkalian angka dengan matriks, maupun perkalian antarmatriks.

1. Penjumlahan dan pengurangan matriks

Penjumlahan dan pengurangan matriks hanya bisa dilakukan jika ordonya sama, misalnya matriks 2 × 2 dikurangkan dengan matriks 2 × 2 lainnya. Elemen yang dijumlahkan atau dikurangkan harus seletak, artinya posisi atau letaknya sama. Perhatikan contoh berikut.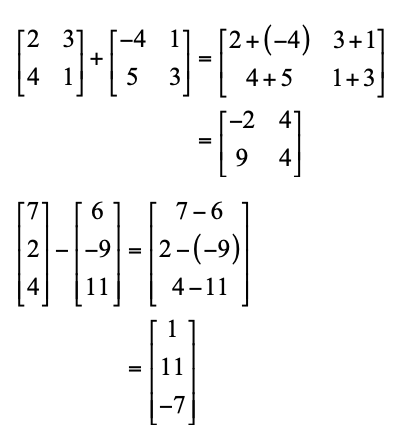

Berdasarkan contoh di atas, terlihat bahwa penjumlahan atau pengurangan matriks tidak mengakibatkan perubahan ordo.

2. Perkalian angka dengan matriks

Semua matriks bisa dikalikan dengan konstanta atau bilangan berapapun. Jika dikalikan dengan suatu konstanta atau bilangan, semua elemen di dalam matriks tersebut harus dikalikan satu per satu dengan konstanta yang dimaksud. Contohnya sebagai berikut.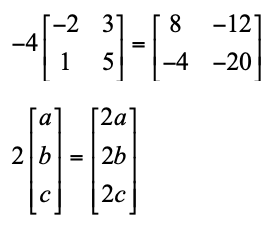

Berdasarkan hasil di atas, ternyata perkalian antara konstanta dan matriks tidak akan mengubah ordo matriks tersebut.

3. Perkalian antara matriks dan matriks

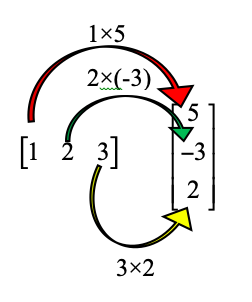
Jika dibandingkan operasi matriks sebelumnya, perkalian antara matriks dan matriks ini terbilang lebih rumit. Untuk mengalikan antara matriks dan matriks, Quipperian harus mengalikan seluruh elemen tiap baris ke-pdengan kolom ke-­p, lalu hasilnya dijumlahkan pada baris yang sama. Misalnya diketahui perkalian matriks sebagai berikut.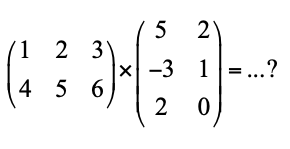

Contoh mengoperasikan perkalian antara dua matriks di atas adalah sebagai berikut.
 

Pembahasan: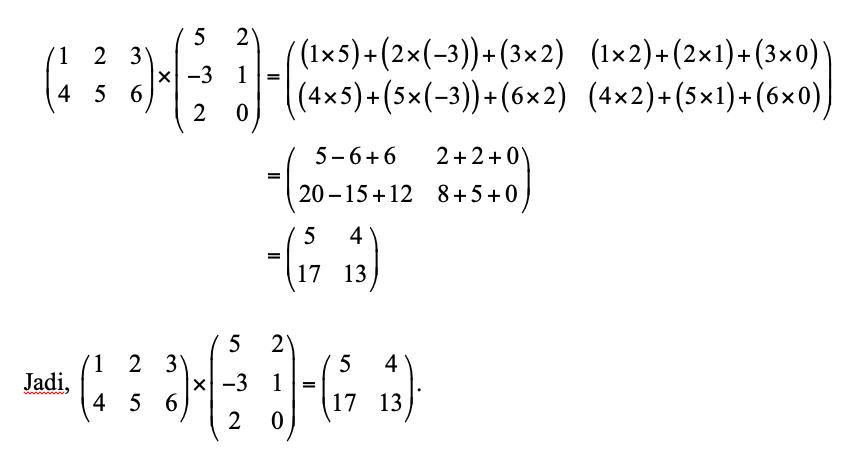

Hal yang harus diingat dari perkalian matriks adalah sifat perkalian matriks tidak berlaku bolak-balik atau  AB ≠ BA.
Agar Quipperian semakin paham dengan pembahasan matriks ini, perhatikan contoh soal berikut.

Contoh Soal 2

Pembahasan:
Sebelum menyelesaikan soal di atas, Quipperian jabarkan kembali persamaannya, yaitu sebagai berikut.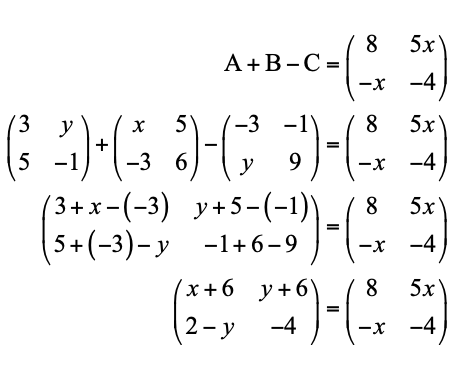

Selanjutnya, tentukan nilai xdan yberdasarkan nilai elemen seletak.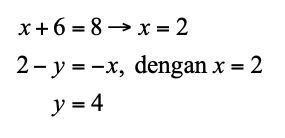

Diperoleh nilai x= 2 dan y= 4. Dengan demikian, x+ 2xy+ y= 2 + 2(2)(4) + 4 = 22.
Jadi, nilai x+ 2xy+ y= 22.

Contoh soal 3

Tentukan nilai 2a²+ b– c  yang memenuhi persamaan matriks berikut.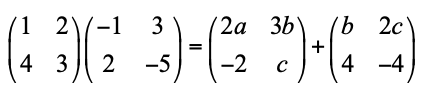

Pembahasan:
Untuk menentukan nilai 2a²+ b– c, Quipperian harus mengalikan matriks-matriks di sisi kiri terlebih dahulu.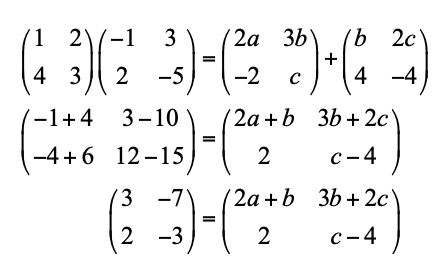

Dari persamaan di atas, diperoleh:
Baris ke-2, kolom ke-2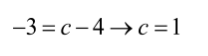

Baris ke-1, kolom ke-2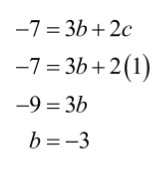

Baris ke-1, kolom ke-1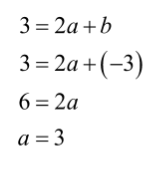

Dengan demikian, nilai 2a²+ b– c= 2(3)²+ (-3) – 1 = 14.
Jadi, nilai 2a²+ b– c= 14.